5.9 VARIAS MUESTRAS INDEPENDIENTES: PRUEBA DE KRAUSKAL-WALIIS

    En unidades anteriores se estudió lo que fue la ANOVA que es un análisis de varianza que compara más de dos muestras, pues en este caso la prueba de Kruskal-Wallis viene siendo el equivalente en los métodos no paramétricos, ya que existe bajo el supuesto de que k ≥ 3. 

    Las hipótesis que se manejan para esta prueba son las siguientes:

• Hipótesis nula: Todas las poblaciones son idénticas.
• Hipótesis alternativa: No todas las poblaciones son idénticas.

    Esta prueba:

• Se puede usar tanto en datos ordinales, de razón o de intervalo.
• Las muestras pueden ser aleatorias independientes de cada una de las k poblaciones.
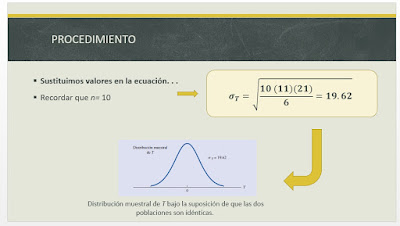
• El estadístico de prueba que se utiliza es el siguiente:

Imagen extraída de la exposición del equipo 10

5.8 OBSERVACIONES PAREADAS: PRUEBA DE WICOLXON

Para explicar este tema, se usaran las diapositivas que el equipo 8 expuso, se va a empezar con una pequeña introducción al tema. 

Con el fin de extender el tema se explicara un ejemplo y los pasos que se llevan a cabo para solucionarlo.

• Primero se inicia por ordenar de menor a mayor los datos y luego asinarles un rango

• Luego se continua realizando la hipótesis para este ejercicio

• Se le asigna un rango empezando por el menor valor al que se le asigna el 1, en caso de que alguno se repita como es el caso del 0.4 que se repite dos veces se divide el rango y quedaría como 3.5 y 3.5  

• Ahora se analiza la hipótesis planteada al principio

• Después de haberse sumado los rangos se procede a aplicar la formula 

• Se sustituyen valores en la ecuación

• Se aplica el estadístico de prueba z y se busca en las tablas el valor de z

• Por ultimo se compara el resultado con las hipótesis y se decide cual aceptar y porque.

5.7 OBSERVACIONES PAREADAS: PRUEBA DE SIGNOS

 

     En temas pasados se hablo respecto a la prueba de signos pero en esta ocasión se explicara un ejercicio. Aunque en clase no se hablo de este tema, es importante incluirlo.

    En el caso de muestras grandes si la hipótesis nula es p= .50 y el tamaño de la muestra es n>20 la distribución muestral del número de signos más se aproxima mediante una distribución normal. 

En un sondeo realizado durante una campaña para elecciones presidenciales se pidió a 200 votantes registrados que evaluaran a los candidatos demócrata y republicano con relación a su política exterior. El resultado obtenido fue: 72 de los encuestados evaluaron mejor al candidato demócrata, 103 evaluaron mejor al republicano y 25 no encontraron diferencia entre los candidatos. ¿Con este sondeo puede observarse que exista una diferencia significativa, entre los candidatos, en términos de la opinión pública acerca de su política exterior?

• Usando las formula y sustituyendo

• Usando el estadístico de  prueba:

    Como se obtiene que valor-p ≤ α= 0.05, se rechaza H nula. Como resultado de este estudio se encuentra que los candidatos difieren en términos de la opinión pública acerca de su política exterior

5.6 DOS MUESTRAS: PRUEBAS DE MANN-WHITNEY-WICOLXON

     En esta ocasión se  hablara de la prueba de Mann-Whitney o prueba de suma de rangos de Wicolxon, ya que fue creada entre Mann, Whitney y Wicolxon.

     La prueba de MWW no requiere que los datos sean intervalos ni que las poblaciones estén distribuidas normalmente.

• Lo único que se pide es que por lo menos la escala de medida sea ordinal  
• La prueba de MWW determina si las dos poblaciones son idénticas
• No se basa en una muestra por pares 
• Se usan datos independientes 

Las hipótesis para esta prueba son:

• H nula: Las dos poblaciones son idénticas 
• H alternativa: Las dos poblaciones son diferentes. 

     En el caso de las muestras pequeñas se usa siempre que los tamaños de las muestras sean menores o iguales a 10. Los pasos para llevar a cabo una muestra pequeña son los siguientes:

• Reunir en una sola columna los datos y ordenarlos de menor a mayor 
• Sumar los rangos de cada muestra por separado

EJEMPLO:

IMAGEN RESCATADA DE EXPOSICIÓN EN CLASE 

• H nula: Las dos poblaciones son idénticas en términos de preparación académica
• H alternativa: Las dos poblaciones no son idénticas en términos de preparación académica

     Por tanto, se rechaza la hipótesis H nula  y se concluye que la población de los estudiantes de la escuela Garfield es diferente de la población de los estudiantes de Mulberry en términos de preparación académica.

5.5 UNA MUESTRA: PRUEBA DE WICOLXON

La prueba de Wicolxon, también llamada prueba de los rangos con signo de Wicolxon es el equivalente a las muestras con pares que se ha estudiado en unidades anteriores, con la diferencia que esta es para datos no paramétricos. 

     

   En este tema como en el de la muestra con pares, cada unidad experimental genera dos observaciones correspondientes 1 a la primera población y la 2 para la segunda población.

Las diferencias entre estas permite apreciar las observaciones de ambas poblaciones.

  

5.4 UNA MUESTRA: PRUEBA DE SIGNOS

     Como se explico en clase la prueba de los signos se utiliza para saber la preferencia u opinión acerca de un producto o tema determinado.

        Sin embargo existen pruebas para muestras pequeñas y muestras grandes.

       A continuación  se muestra una prueba de signos para una sola muestra, la cual fue extraída de lo explicado en clase.

     Para este tipo de pruebas se utiliza un estadístico de prueba  z, ya que se usan las tablas de distribución normal 

         En este caso el resultado de la prueba fue que las opiniones son diferentes, por lo tanto no existen argumentos para decir que son iguales. Igual se puede identificar en la distribución normal como quedan los signos.

5.3 PRUEBAS DE CORRIDAS PARA ALEATORIEDAD

    Las pruebas de corridas para aleatoriedad también son conocidas como PRUEBA DE LOS SIGNOS. 

     Se utiliza con frecuencia para investigaciones de mercado, se usa un muestra de n clientes para que indiquen su preferencia entre 2 productos puede ser entre dos marcas de cereales, detergentes, refrescos, etc.

     Las preferencias que tenga el consumidor son datos nominales ya que simplemente escoge es aquí cuando entra la prueba de los signos, ya que se debe determinar si existe diferencia entre las preferencias de dichos consumidores, o si existe diferencia entre los productos o marcas.

     Por ejemplo si damos a probar a 5 personas el refresco X y el refresco Y siendo nosotros productores del refresco X:

• Cada que un consumido escoja nuestro producto se le asignara el signo +
• Cada que un consumidor escoja el otro producto se le asignara el signo -

Este es solo un ejemplo, ya que la prueba de signos puede clasificarse para:

1. Muestras pequeñas 
2. Muestras grandes 

En el caso de las muestras pequeñas es siempre que n ≤ 20, a continuacion se muestra una tabla de dos marcas de refresco:

imagen rescatada de la exposición del equipo 3